Phân tích hiệu suất với Data Envelopment Analysis

Giới thiệu

Trong thế giới hiện đại, các Data Scientist đóng vai trò quan trọng trong việc giúp các tổ chức tối ưu hóa hoạt động và đạt được mục tiêu chiến lược. Một trong những công cụ quan trọng trong bộ công cụ của họ là phân tích hiệu suất, một yếu tố then chốt để đảm bảo rằng các nguồn lực được sử dụng một cách hiệu quả nhất. Phân tích hiệu suất cho phép các Data Scientist đánh giá và cải thiện hoạt động của các tổ chức thông qua việc đo lường và phân tích các chỉ số hoạt động quan trọng.

Tại sao phân tích hiệu suất là cần thiết?

• Tối Ưu Hóa Quy Trình: Phân tích hiệu suất giúp xác định các quy trình kém hiệu quả, từ đó đề xuất các biện pháp cải tiến nhằm tối ưu hóa quy trình làm việc và giảm lãng phí tài nguyên.

• Ra Quyết Định Dựa trên Dữ Liệu: Đưa ra quyết định chiến lược dựa trên dữ liệu chính xác và đáng tin cậy thay vì cảm tính hoặc dự đoán. Phân tích hiệu suất cung cấp cái nhìn rõ ràng về hoạt động và giúp đưa ra các quyết định thông minh hơn.

• Đo Lường Thành Công: Hiểu được các yếu tố chính tạo ra thành công giúp tổ chức duy trì và phát triển các yếu tố đó, đồng thời điều chỉnh các chiến lược để cải thiện hiệu quả.

• Cải Thiện Hiệu Quả Chi Phí: Giúp nhận diện các cơ hội tiết kiệm chi phí và tối ưu hóa ngân sách bằng cách phân tích cách các tài nguyên được phân bổ và sử dụng.

• Tăng Cường Cạnh Tranh: Hiểu rõ điểm mạnh và điểm yếu của mình so với đối thủ cạnh tranh, từ đó phát triển các chiến lược cải thiện và gia tăng lợi thế cạnh tranh.

Data Envelopment Analysis (DEA)

Phân Tích Hiệu Suất Dựa trên Data Envelopment Analysis (DEA) là một phương pháp phân tích hiệu suất và đánh giá hiệu quả của các tổ chức, đơn vị, hoặc quy trình dựa trên các dữ liệu đầu vào và đầu ra. Phương pháp này được phát triển bởi Charnes, Cooper, và Rhodes vào năm 1978 và đã nhanh chóng trở thành công cụ quan trọng trong quản lý và nghiên cứu hoạt động.

DEA cung cấp một cách tiếp cận phi tham số để đánh giá hiệu quả, khác với các phương pháp phân tích khác thường dựa trên các giả định và mô hình thống kê cụ thể. Thay vào đó, DEA so sánh các đơn vị đánh giá (hay còn gọi là các đơn vị quyết định, DMUs - Decision Making Units) với nhau dựa trên cách mà các tài nguyên đầu vào của chúng được chuyển đổi thành các kết quả đầu ra.

Cơ bản về Phân tích hiệu suất

Khi chúng ta đánh giá hiệu suất của một giải pháp, chúng ta cần phải so sánh kết quả đầu vào và đầu ra. Ví dụ như khi chúng ta sản xuất một sản phẩm A với chi phí X/sản phẩm và mang lại lợi nhuận Y/Sản phẩm. Để đánh giá hiệu quả cơ bản nhất, ta có thể so sánh Lợi nhuận/ Chi phí xem hiệu quả của nó mang lại bao nhiêu? Giả sử sản phẩm A đó:

• Chi phí sản xuất 20,000 đồng / sản phẩm
• Lợi nhuận mang lại 12,000 đồng / sản phẩm

Hiệu quả có thể tính đơn giản là 12,000/20,000 = 0.6

Hay tổng quát hơn, với các yếu tố đầu vào được gọi là Input và đạt được kết quả đầu ra là Output, hiệu quả có thể được tính theo công thức

$$\frac{Output}{Input}$$

Input có thể là 1 hoặc nhiều yếu tố và Output cũng có thể là một hoặc nhiều yếu tố. Để đi sâu hơn, chúng ta sẽ đến các ví dụ minh họa ở phần tiếp theo

Bài toán Phân tích hiệu suất

Bài toán 1 input và 1 output

Phát biểu bài toán

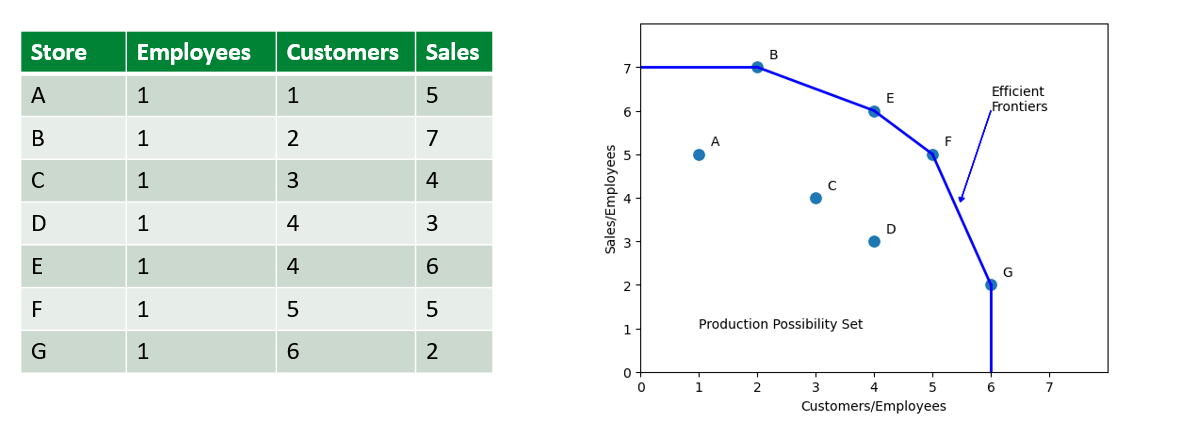
Ví dụ một nhãn hàng có 8 cửa hàng được gán nhãn là A, B, C, D, E, F, G, H với Input là Số lượng nhân viên (Employee) của cửa hàng đó và Output là số lượng hàng bán được (Sales) của cửa hàng. Hệu suất của cửa hàng được tính theo công thức đơn giản là Sales/Employees. Kết quả thu được cửa hàng B có hiệu suất cao nhất là 1 và cửa hàng F có hiệu suất thấp nhất là 0.4

Ví dụ một input và một output

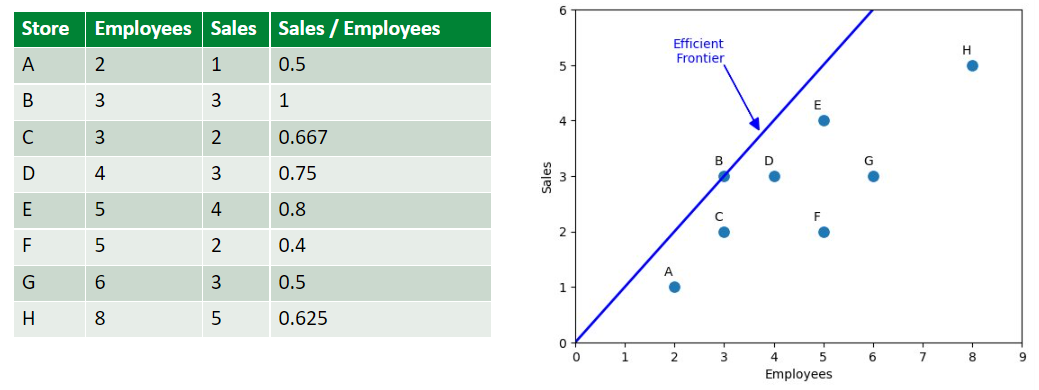
Phân tích đánh giá

Ta có thể biểu diễn mối tương quan giữa Input và Output bằng scatterplot. Độ dốc của đường nối với mỗi điểm và gốc tọa độ $O(0,0)$ tương ứng với $Sales/ Employee$ ( hiệu quả). Trong hình trên ta có thể tính được đường thằng $OB$ có dạng $y=1x$, do đó hiệu suất của B là 1. ​

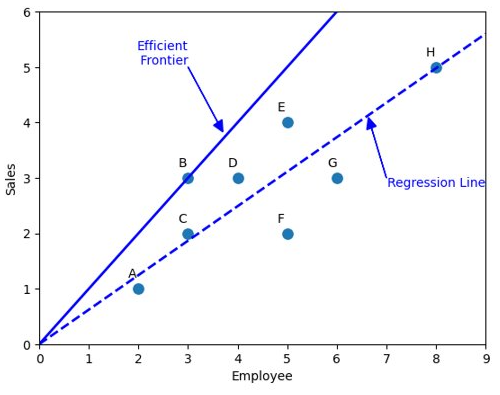
Đường có độ dốc cao nhất (đi qua gốc tọa độ và điểm B) được gọi là Efficient Frontier (Đường biên hiệu quả).​ Các điểm sẽ nằm cùng 1 phía so với đường thẳng, hoặc ở trên, hoặc ở dưới.​ Nếu chúng ta vẽ Output là trục tung và Input là trục hoành thì các điểm sẽ nằm phía dưới đường biên hiệu quả. Ngược lại nếu chúng ta vẽ Output là trục hoành và Input là trục tung thì các điểm sẽ nằm phía trên của đường biên hiệu quả.

Chúng ta có thể vẽ một đường thống kê hồi quy $y=0.622x$ để ước lượng mối quan hệ tuyến tính giữa Input và Output.​ Đường hồi quy này đi qua chính giữa của tập dữ liệu, do đó chúng ta có thể xem các điểm ở phía trên đường là hiệu quả tốt và điểm dưới là chưa tốt, khoảng cách giữa điểm tới hình chiếu của điểm đó trên đường hồi quy chính ta mức độ hiệu quả/không hiệu quả​ so với trung bình. Trong ví dụ trên, chúng ta có thể thấy điểm H gần với trung bình nhất.

Efficient Frontier và Regression Line

So sánh với đường biên hiệu quả

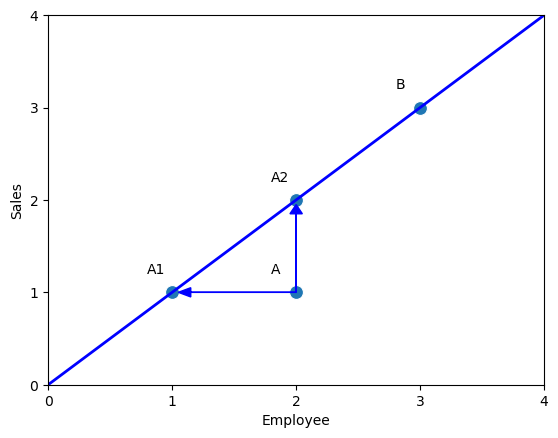
Với cửa hàng A, có hai cách để so sánh với đường biên. Bằng cách chiếu theo trục tọa độ, chúng ta có hai điểm A1 và A2​

• Với điểm A2, để đạt được hiệu suất như B mà vẫn giữ nguyên số lượng nhân viên, chúng ta cần phải cố gắng tăng Sale lên 2​
• Với điểm A1, nếu muốn giữ nguyên sale mà vẫn muốn đạt được hiệu suât cao, chúng ta cần phải cắt giảm nhân sự xuống 1.

Ngoài ra, bất cứ điểm nào nằm trong đoạn A1A2 cũng là kết quả tối ưu cho cửa hàng B, đối với các điểm này, chúng ta cần phải thay đổi cả giá trị Sale lẫn Employee.

So sánh với đường biên hiệu quả

Bài toán 2 input và 1 output

Phát biểu bài toán

Trong ví dụ đầu, chúng ta đã làm quen với đầu vào là Số lượng nhân sự của một cửa hàng và đầu ra là số sale của cửa hàng đó. Ở ví dụ này, chúng ta sẽ làm quen với việc thêm một đầu vào là Diện tích mặt bằng của cửa hàng. Để tiện lợi cho việc tính toán, chúng ta chuẩn hóa số lượng Sale ở các cửa hàng về 1

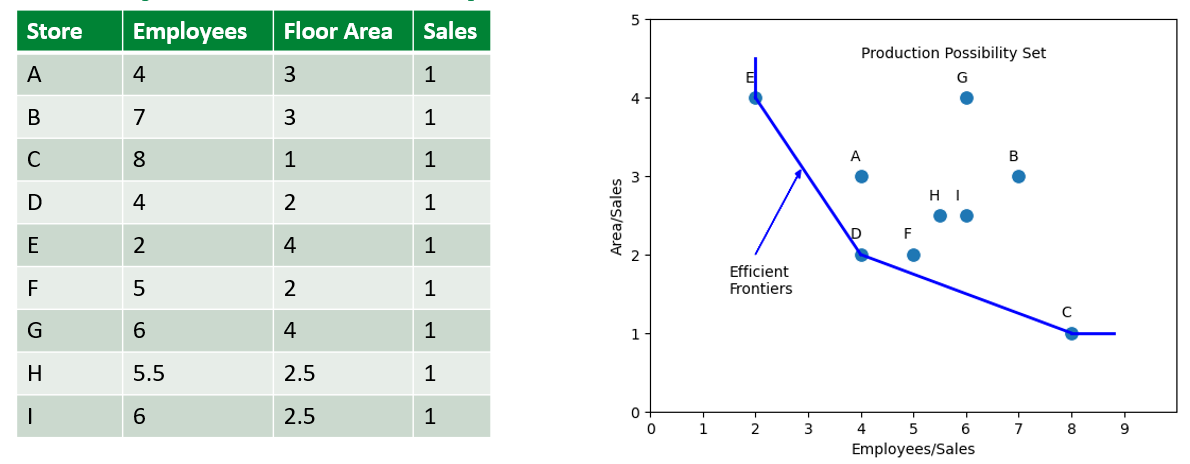
Phân tích đánh giá

Với bài toán này, ta vẽ scatterplot với 2 trục tung và hoành lần lượt là $\frac{Input_1}{Output} = \frac{Employees}{Sales}$ và $\frac{Input_2}{Output} = \frac{Floor Area}{Sales}$.

Đường biên hiệu quả trong trường hợp này là đường gấp khúc đi qua 3 điểm E, D, C. Đường này bao tất cả các điểm nằm trong nó, tất cả các điểm còn lại đều nằm cùng phía và nằm phần trên so với Đường biên hiệu quả

Vùng chứa các điểm ở trong này được gọi là Production Possibility Set.

So sánh với đường biên hiệu quả

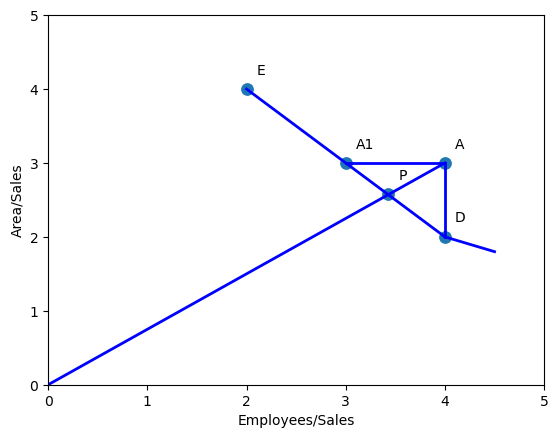
Với cửa hàng A, ta có thể nói rằng hai cửa hàng E, D là cửa hàng tham chiếu của nó, nghĩa là để tối ưu hiệu suất của cửa hàng A, ta cần phải dựa trên hiệu quả của cửa hàng E và D. Để làm được điều này, chúng ta vẽ đường thẳng OA cắt đường biên E, D tại P có $\frac{Employees}{Sales}$ và $\frac{Area}{Sales}$ lần lượt là 3.43 và 2.58. Do đó, hiệu quả của A sẽ được tính theo cách hình học như sau: $\frac{OP}{OA} = \frac{4.29}{5} = 0.858$

Để tối ưu cửa hàng A, ta có các phương án sau

• Giảm employees/sales về 3.43 và areas/sales về 2.58
• Giữ nguyên employee và giảm area về điểm D
• Giữ nguyên area và giảm employee về điểm A1

Bài toán 1 input và 2 output

Phát biểu bài toán

Ngược lại với ví dụ trên, chúng ta sẽ đến ví dụ với một input là số lượng nhân viên của cửa hàng và hai output là số lượng khách hàng và số sales của cửa hàng đó. Tương tự để thuận tiện cho việc tính toán, chúng ta sẽ chuẩn hóa số lượng nhân viên về 1.

Phân tích đánh giá

Với bài toán này, ta vẽ scatterplot với 2 trục tung và hoành lần lượt là $\frac{Output_1}{Input} = \frac{Customers}{Employees}$ và $\frac{Output_2}{Input} = \frac{Sales}{Employees}$.

Đường biên hiệu quả trong trường hợp này là đường gấp khúc đi qua các điểm B, E, F, G.Đường này bao tất cả các điểm nằm trong nó, tất cả các điểm còn lại đều nằm cùng phía và nằm phần dưới so với Đường biên hiệu quả

Vùng chứa các điểm ở trong này được gọi là Production Possibility Set.

Chúng ta để ý rằng đối với Dữ liệu tập trung Input thì đường biên sẽ nằm ở dưới, và cố gắng tối ưu tỉ lệ Input/Output nhỏ nhất có thể. Còn đối với dữ liệu tập trung Output thì đường biên sẽ nằm ở trên thể hiện rằng Output/Input càng cao thì càng tối ưu

So sánh với đường biên hiệu quả

So sánh với đường biên hiệu quả

Ta có thể nhận thấy B là điểm tham chiếu của cửa hàng A, từ B ta kẻ đường thẳng song song với trục hoành, sau đó vẽ đường thằng OA cắt đường song song tại Q, hiệu quả của cửa hàng A được tính theo $\frac{OA}{OQ} = 0.714$.

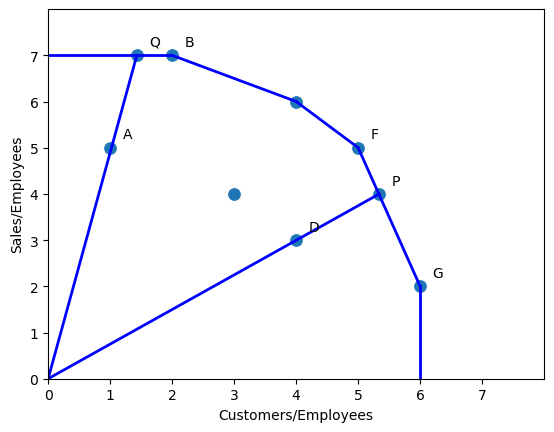
Tương tự ta có F,G là hai điểm tham chiếu của D, ta vẽ đường OD cắt FG tại P. Hiệu quả của cửa hàng D được tính bằng $\frac{OD}{OP}=0.75$

Bài toán Nhiều input và Nhiều output

Phát biểu bài toán

Dữ liệu các bệnh viện được đánh nhãn từ A đến L có các Inputs là Số lượng Bác sĩ (Doctors) và số lượng Y tá (Nurses), Outputs là số lượng bên nhân Ngoại trú (Outpatients) và số lượng bệnh nhân nội trú (Inpatients).

Bảng ví dụ về thông tin các bệnh viện với nhiều input và nhiều output

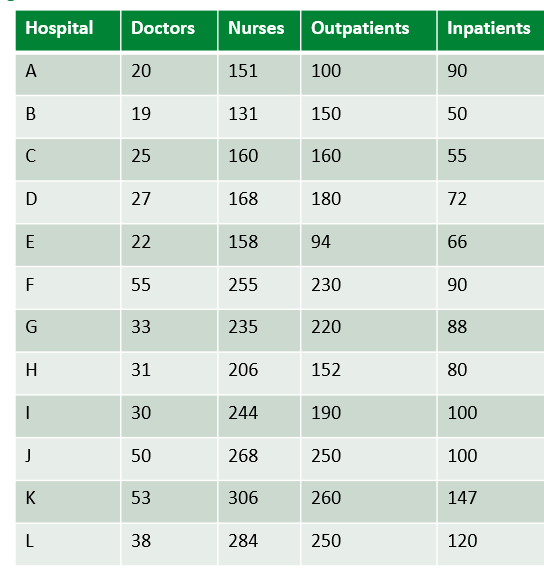
Phân tích đánh giá

Công thức tính hiệu quả được tính như sau

$$\Large \frac{Outpatents * u_1 + Inpatients * u_2}{Doctors * v_1 + Nurses * v_2}$$

Trong đó $u_1, u_2, v_1, v_2$ là các trọng số tương ứng với các Input và Output. Người quản lý có thể dựa vào kinh nghiệm để lựa chọn một tỉ lệ thích hợp. Giả sử chúng ta chọn tỉ lệ $u_1:u_2 = 1:3$ và $v_1:v_2=5:1$, Hiệu suất của các bệnh viện sẽ được tính và chuẩn hóa về 1(Bằng cách chia cho bệnh viện có hiệu suất cao nhất)

Bảng tính hiệu quả dựa trên các trọng số cho trước

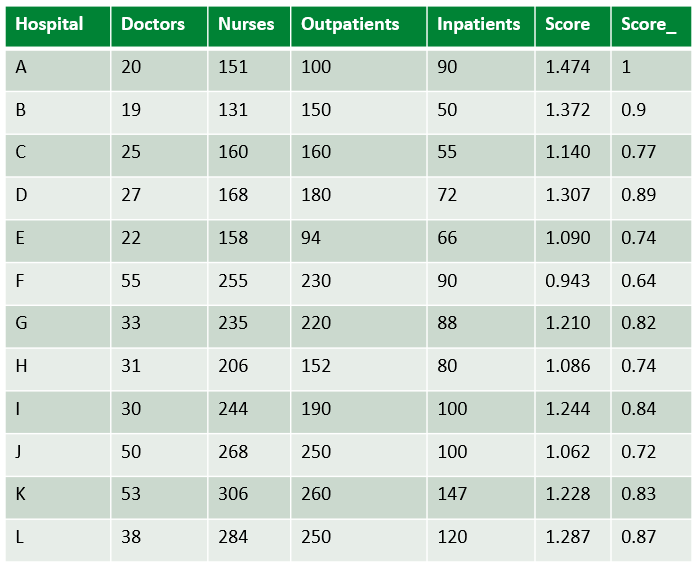
Kết quả cho thấy bệnh viện A được đánh giá cao nhất là 1 sau đó là bệnh viện B là 0.9, bênh viện F thấp nhất là 0.64.

Có cách chọn các tham số nào để bệnh viện B có thể có score tốt hơn 0.9 không?

Một trong những cách có thể chọn tham số cục bộ để tối ưu hiệu suất cho từng bệnh viện là CCR model

CCR model

CCR model được đề xuất bởi Charnes, Cooper và Rhodes vào năm 1978. CCR là một trong các phương pháp phân tích DEA. được sử dụng để đánh giá hiệu quả của các đơn vị ra quyết định (Decision Making Units - DMUs) khi có nhiều đầu vào và đầu ra. Ngoài phương pháp CCR, DEA còn có các biến thể như:

• BCC (Banker, Charnes, Cooper)
• SBM (Slacks-Based Measure)

Trong phạm vi bài viết này, mình tập trung vào CCR cơ bản.

CCR đưa ra hai khái niệm Virtual input và Virtual output

$$\Large Virtual\ input = v_1*x_1 + ... + v_m * x_m \\ \Large Virtual\ output = u_1*y_1 + ... + u_s * y_s$$

Trong đó:

• $v_1,...,v_m$ là trọng số tương ứng với các input $x_1,...,x_m$
• $u_1,...,u_s$ là trọng số tương ứng với các output $y_1,...,y_s$

Mô hình sử dụng phương pháp Quy hoạch Tuyến tính (Linear Programming) để tối ưu hiệu suất cho từng đơn vị (Decision Marking Unit) theo tỉ lệ

$$\Large DMU = \frac{virtual\ output}{virtual\ input}$$

Với mô hình này, mỗi bệnh viện sẽ có bộ trọng số tối ưu khác nhau

Công thức cơ bản

Để đơn giản, ta chỉ ví dụ việc tối ưu cho 5 bệnh viện A, B, C, D, E.

Bảng ví dụ về thông tin 5 bệnh viện với nhiều input và nhiều output

Để tìm các trọng số sao cho tối ưu bệnh viện A DMU(A). Chúng ta cần giải bài toán tối ưu

$$Maximize\ \frac{100u_1 + 90u_2}{20v_1 + 141v_2}$$

Thỏa mãn các ràng buộc

$$\frac{100u_1+90u_2}{20v_1+151v_2}\le 1 (A)$$ $$\frac{150u_1+50u_2}{19v_1+131v_2}\le 1 (B)$$ $$\frac{160u_1+55u_2}{25v_1+160v_2}\le 1 (C)$$ $$\frac{180u_1+72u_2}{27v_1+168v_2}\le 1 (D)$$ $$\frac{94u_1+66u_2}{22v_1+158v_2}\le 1 (E)$$

Bài toán trên có thể chuyển đổi thành bài toán quy hoạch tuyến tính sau.

$$Maximize\ 100u_1 + 90u_2$$

Sao cho

$$(100u_1+90u_2) - (20v_1+151v_2) \le 0 (A)$$ $$(150u_1+50u_2)-(19v_1+131v_2) \le 0 (B)$$ $$(160u_1+55u_2)-(25v_1+160v_2)\le 0 (C)$$ $$(180u_1+72u_2)-(27v_1+168v_2)\le 0 (D)$$ $$(94u_1+66u_2)-(22v_1+158v_2)\le 0 (E)$$ $$20v_1 + 151v_2 = 1; u_1, u_2, v_1, v_2 \ge 0$$

Chúng ta có thể sử dụng thư viện pulp để giải quyết bài toán trên. Kết quả thu được cho Bệnh viện A

• $u_1 = 0.004176, u_2 = 0.006471$
• $v_1 = 0.05000, v_2 = 0.000000$

Áp dụng cho các bệnh viện khác ta tìm được các trọng số như sau. Dưới đây là code của mình sử dụng pandas và pulp

from pulp import LpMaximize, LpProblem, LpStatus, lpSum, LpVariable, LpMinimize
import pandas as pd
def CCR_model(_df,col_name="", type='input', Inputs=[], Outputs=[]):
    df = _df.copy()
    df.reset_index(drop=True, inplace=True)
    model = LpProblem(name="small-problem", sense=LpMaximize)
    Inputs_Variables = []
    Outputs_Variables = []
    for input in Inputs:
        var = LpVariable(name=input, lowBound=0)
        Inputs_Variables.append(var)
    for output in Outputs:
        var = LpVariable(name=output, lowBound=0)
        Outputs_Variables.append(var)
    df['Inputs'] = df.apply(lambda x: lpSum([var * x[name] for (var, name) in zip(Inputs_Variables, Inputs)]), axis=1)
    df['Outputs'] = df.apply(lambda x: lpSum([var * x[name] for (var, name) in zip(Outputs_Variables, Outputs)]), axis=1)
    df['Outputs - Inputs'] = df.apply(lambda x: x['Outputs'] - x['Inputs'] <= 0, axis=1)
    df['Inputs_St'] = df['Inputs'].apply(lambda x: x==1)
    df['Outputs_St'] = df['Outputs'].apply(lambda x: x==1)

    
    def solve(k):
        pis = []
        if type =='input':
            model = LpProblem(name=f"small-problem_{k}", sense=LpMaximize)
        if type =='output':
            model = LpProblem(name=f"small-problem_{k}", sense=LpMinimize)
        for i,sj in enumerate(df['Outputs - Inputs'].values):
            model += sj
        if type=='input':
            model+= df['Inputs_St'].values[k]
            model+= df['Outputs'].values[k]
        if type=='output':
            model+= df['Outputs_St'].values[k]
            model+= df['Inputs'].values[k]
        status = model.solve()
        for (name, constraint) in model.constraints.items():
            # print(f"{constraint}: {constraint.pi}")
            pis.append(constraint.pi)
        # print(Inputs_Variables[0].varValue)
        return status, model.objective.value(), model, pis
    
    weights = []
    models = []
    datas =[]
    for i in range(df.shape[0]):
        status, val, model, pis = solve(i)
        weight = {}
        for variable in model.variables():
            weight[variable.name] = variable.varValue
        weights.append(weight)
        datas.append(pis)
    output = pd.DataFrame(datas,columns=df[col_name].to_list() +['Efficiency'])
    output = output.apply(lambda x: round(x, 4))
    output[col_name] = df[col_name]
    output = output[[col_name, 'Efficiency']+df[col_name].to_list()]
    return output, models ,weights

Kết quả sẽ trả về 2 biến chính

• weights: Trọng số cho từng bệnh viện
• outputs: Hiệu quả đã được tối ưu

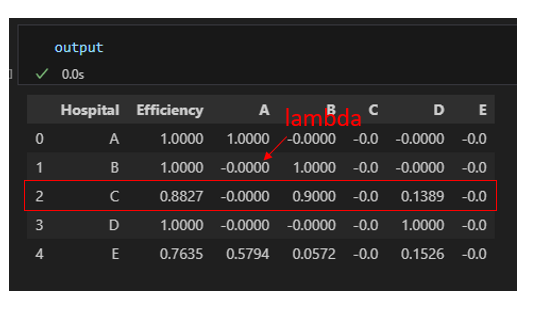
output,_, weights = CCR_model(dfx, "Hospital", 'input',["Doctors",'Nurses'], ['Outpatients', 'Inpatients'])
pd.DataFrame(weights)[["Doctors",'Nurses', 'Outpatients', 'Inpatients']]

Bảng trọng số cho các input và output

So với kết quả của phương pháp chọn sẵn các trọng số, phương pháp CCR giúp tính toán hiệu suất tối ưu hơn, các điểm B và D được kéo về 1 như điểm A

So sánh cách tính hiệu quả mới theo cách tối ưu (Bên trái) và cách tính hiệu quả với trọng số cho trước(Bên phải)

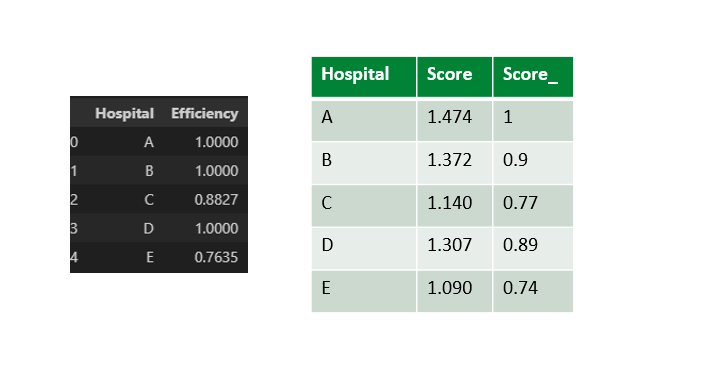
Đối với bảng output, với Bệnh Viện C ta có chỉ số DMU < 1. Để phân tích hiệu suất, ta so sánh với các Bệnh viện B, D có các giá trị lambda khác 0. Lúc này B và D được gọi là 2 điểm tham chiếu của C

Hiệu quả(Efficiency) của các bệnh viện và các điểm tham chiếu của nó cùng với các chỉ số lambda

Phân tích tối ưu

Để tối ưu cho bệnh viện C. Ta lập bảng tính toán như sau

Bảng phân tích hiệu quả

Trong đó:

• Hospital B, D là 2 bệnh viện tham chiếu
• Value là từng giá trị Input, Output cho các bệnh viện
• Lambda là chỉ số lambda được lấy từ bảng output, đối với bệnh viện B là 0.9 và D là 0.1389
• Total = Value x Lambda
• Total Sum bằng Tổng của Total bệnh viện B và bệnh viện D
• Diff được tính bằng Value của cửa hàng C trừ với Total Sum

Kết quả phân tích cho thấy Bệnh viện C đang dư thừa 4.15 Bác sĩ và 18.76 Y tá cho việc điều trị 160 Bệnh nhân ngoại trú và 55 Bệnh nhân nội trú.

Tài liệu tham khảo

• Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software